
آشنایی با رگرسیون خطی در دنیای یادگیری ماشین
در این مقاله میخوانید
رگرسیون خطی یکی از اولین ایستگاهها در مسیر یادگیری ماشین و هوش مصنوعی است. همانطور که پیش از این در مقاله «هوش مصنوعی چیست؟» بیان کردیم، هوش مصنوعی روشها و حوزههای گوناگونی دارد. یادگیری ماشین یکی از زیرمجموعههای مهم و کلیدی در دنیای هوش مصنوعی است. همچنین در مقاله «صفر تا صد یادگیری ماشین» بررسی کردیم که یادگیری نظارت شده یکی از انواع روشهای یادگیری ماشین است.
مروری بر مفهوم یادگیری نظارت شده در دنیای یادگیری ماشین
پیش از آنکه به سراغ رگرسیون خطی برویم، بهتر است مفهوم یادگیری نظارت شده را مرور کنیم. یادگیری نظارتشده یا Supervised Learning روشی در یادگیری ماشین است که در آن مدل با استفاده از دادههای دارای برچسب یا خروجی مشخص، آموزش میبیند تا الگوهای موجود را شناسایی کند و سپس برای دادههای جدید پیشبینیهایی انجام دهد.
بهعنوان مثال، اگر مجموعهای از دادهها شامل قد و وزن افراد همراه با برچسبهایی مانند “ورزشکار” یا “غیرورزشکار” را داشته باشیم، مدل با تحلیل این دادهها قادر خواهد بود دستهبندی مناسبی برای افراد جدید با مشخصات مشابه ارائه دهد. یکی از الگوهایی که مدل میتواند بر اساس آن عمل کند، رگرسیون خطی است.
رگرسیون چیست؟
رگرسیون یا برونیابی یک تکنیک آماری و یادگیری ماشین است که رابطه بین متغیرهای مستقل و وابسته را مدلسازی میکند. این روش برای پیشبینی مقادیر خروجی براساس ورودیهای جدید با استفاده از الگوهای کشفشده در دادههای قبلی به کار میرود. حتی اگر با حوزه هوش مصنوعی و یادگیری ماشین آشنایی نداشته باشید، ممکن است با رگرسیون آشنا باشید. دانشجویان رشتههای فنی و مهندسی در درس محاسبات عددی با این مفهوم آشنا میشوند. دانشجویان مدیریت و اقتصاد نیز در درس اقتصاد سنجی از رگرسیون استفاده میکنند.
روابط بین متغییرهای مستقل و وابسته میتواند به شیوههای مختلفی باشد، سادهترین الگو، الگوی خطی است.
رگرسیون خطی چیست؟
رگرسیون خطی یک روش آماری و یادگیری ماشین است که برای مدلسازی و پیشبینی رابطه بین متغیر وابسته و یک یا چند متغیر مستقل استفاده میشود.
در رگرسیون خطی، فرض بر این است که رابطه بین متغیرها به صورت خطی است؛ یعنی تغییرات متغیر مستقل بهصورت خطی بر متغیر وابسته تأثیر میگذارد. در سادهترین حالت، رگرسیون خطی تنها یک متغیر مستقل دارد و مدل آن به شکل یک خط مستقیم نمایش داده میشود. این خط، بهترین خطی است که میتواند دادهها را بهطور تقریبی توصیف کند، بهطوری که فاصله دادهها تا خط حداقل باشد.
معادله خطی ساده این مدل به شکل زیر است:
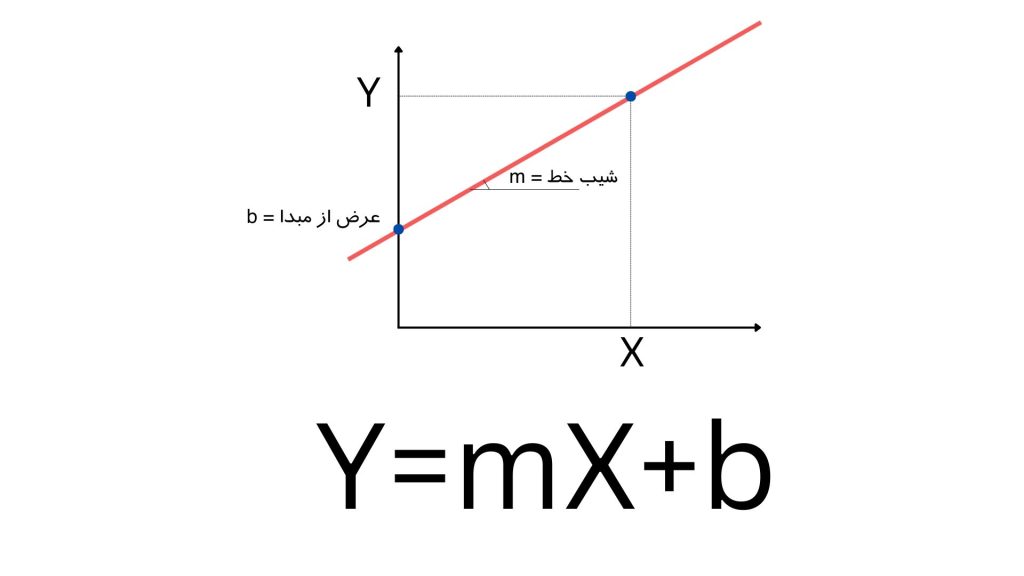
همانطور که در راهنمایی خواندهایم، اگر شیب خط و عرض از مبدا را داشته باشیم، میتوانیم فرمول خط را بنویسیم. بر اساس این فرمول، هر X را که داشته باشیم، میتوانیم Y آن را نیز پیدا کنیم.
رگرسیون چه کاری انجام میدهد؟
رگرسیون یا برونیابی حالتی را توصیف میکند که شما مجموعه ای از نقاط ( یعنی X و Y ها را) دارید که شبیه به یک خط به نظر میرسند ( نیازی نیست حتما روی یک خط باشند) و اگر شما بتوانید فرمول آن، یعنی m و b را کشف کنید، آنگاه هر X دیگری به شما بدهند، میتوانید Y را تخمین بزنید. به شکل زیر توجه کنید. بر روی صفحه زیر تعدادی نقطه (x,y) وجود دارد. به نظر میرسد که همه آنها حول یک خط قرار دارند.

در تصویر بالا دو خط زرد و قرمز ترسیم شده است. سوال این است که کدام یک از این دو خط( یا سایر این خط هایی که رسم نشده است) بهترین خط هستند؟ رگرسیون فرآیندی است که بهترین خط، یعنی خطی که بیشترین تطابق را دارد برای شما پیدا میکند.
انواع رگرسیون خطی
همانطور که گفتیم، رگرسیون خطی حالتی است که ما فرض کردهایم رابطه بین متغییر مستقل و وابسته خطی است. با این وجود حالتها و انواع مختلفی برای رگرسیون وجود دارد. در ادامه برخی از انواع رگرسیون خطی را بررسی میکنیم.
رگرسیون خطی ساده
رگرسیون خطی ساده یا Simple Linear Regression همانطور که از نامش پیداست، سادهترین روش است. در این حالت تنها یک متغیر وابسته و یک متغیر مستقل وجود دارد. یعنی دقیقا با رابطه Y=mX+b
رگرسیون خطی چندگانه
رگرسیون خطی چندگانه یا Multiple Limear Regression حالتی است که متغییر وابسته، به چند متغیر مستقل وابسته است. در این حالت رابطه خطی چیزی شبیه به فرمول Y=mX+nZ+b است. در این فرمول دو متغیر مستقل X و Z و متغیر وابسته Y وجود دارد.
رگرسیون خطی چه کاربردی دارد؟
رگرسیون بر اساس دادههای برچسب دار قبلی ( یعنی متغیرهای مستقلی که متغیر وابسته آنها را نیز داریم) میتواند برای دادههای جدید نیز پاسخ تولید کند.
به عنوان مثال تصور کنید شما لیستی از قیمت و ویژگیهای دهها خودرو دارید. ویژگیهای خودرو ، مثلا مدل خودرو، سال ساخت، کارکرد خودرو، رنگ شدگی و … به عنوان متغیرهای مستقل هستند. قیمت خودرو نیز به عنوان متغیر وابسته یا همان برچسب داده وجود دارند.
رگرسیون خطی یک رابطه خطی میان دادههای موجود پیدا میکند. این رابطه خطی در واقع یک همان فرمول خط است. پس از این که این رابطه کشف شد، حالا شما میتوانید با دادن یک خودرو جدید، بر اساس این فرمول، قیمت آن را پیشبینی کنید. بسیاری از ما هنگامی که میخواهیم خودرو یا خانه بخریم، در ذهنمان به صورت تقریبی از همین کار استفاده میکنیم. هرچند که سراغ فرمولها نمیرویم.
رگرسیون خطی در یادگیری ماشین
رگرسیون در دنیای آمار کاربرد بسیاری دارد. اما همین روش ساده در دنیای هوش مصنوعی و یادگیری ماشین میتواند بسیار قدرتمند باشد. اما چرا؟
محدودیتهای محاسبه و پردازش سبب میشود که هنگامی که میخواهیم از رگرسیون خطی استفاده کنیم، تنها بتوانیم تعداد محدودی داده قبلی را بررسی کنیم و همچنین متغیرهای کمتری را میتوانیم بررسی کنیم. به عنوان نمونه، در مثال قیمت خودرو، شاید شما بتوانید دهها یا نهایتا چند صد قیمت خودرو را بررسی کنید. یا نهایتا ده فاکتور یا متغیر مستقل را در قیمت خودرو بررسی کنید.
اما در دنیای یادگیری ماشین، شما میتوانید دهها هزار خودرو را بررسی کنید و برای هر خودرو صدها متغیر را مورد بررسی قرار دهید. در این حالت است که دقت پیشبینی شما بسیار افزایش مییابد.
نحوه عمل کرد رگرسیون خطی چگونه است؟
در رگرسیون خطی، هدف اصلی پیدا کردن خطی است که به بهترین شکل ممکن رابطه بین متغیرهای مستقل و وابسته را توصیف کند. این خط که به آن «خط رگرسیون» گفته میشود، باید به گونهای باشد که کمترین فاصله را از نقاط دادهها داشته باشد. برای رسیدن به این هدف، چندین مرحله وجود دارد:
۱. تعریف معادله خط رگرسیون
در رگرسیون خطی ساده، معادله خط بهصورت زیر است:
y=b0+b1x
که در آن:
- y متغیر وابسته (پیشبینیشده) است.
- x متغیر مستقل است.
- b0 عرض از مبدأ (مقدار y وقتی x=0 است) است.
- b1 ضریب شیب خط است که نشاندهنده تأثیر x بر y میباشد.
در رگرسیون خطی چندگانه، معادله به شکل زیر گسترش مییابد:
y=b0+b1x1+b2x2+..bnxn
که در آن x1 و x2 و … تا xn متغیرهای مستقل هستند و b1 و b2 و …تا bn ضرایب مربوط به هر متغیر میباشند.
۲. تعریف تابع هزینه (Cost Function)
تابع هزینه به ما کمک میکند که بهترین ضرایب یا همان b0 و b1 و b2 و … را پیدا کنیم. در واقع شما میتوانید هزاران ترکیب از ضرایب مختلف قرار دهید و یک خط رگرسیون ایجاد کنید. اما تابع هزینه این امکان را به شما میدهد که ضرایبی را پیدا کنید که در نهایت دقیقترین پیشبینی را به شما بدهد. دقیقترین پیشبینی حالتی بدست میآید که خط نزدیک ترین فاصله را به نقاط موجود داشته باشد.
در واقع فاصله ی بین خط و نقاط را میتوان به عنوان خطا یا Error در نظر گرفت. تابع هزینه میخواهد این ارور را به کمترین میزان برساند. آنهم نه فقط برای یک نقطه، بلکه برای تمامی نقاط. راههای مختلف و توابع مختلفی برای این کار هدف وجود دارد. یکی از راههای معروف و پر طرفدار استفاده از روش «میانگین مربعات خطا» یا MSE است. این روش فاصله عمودی هر نقطه با خط را حساب میکند و به توان تو میرساند ( با به توان دو رساندن، حساسیت بیشتر میشود) و سپس همه این فاصلهها را با هم جمع میکند. سپس این مجموع را به تعداد نقاط تقسیم میکند. هرچه این MSE کمتر باشد، یعنی خط ما دقیقتر است.
به زبان ریاضی فرمول میانگین مربعات خطا برابر است با
MSE= 1/n (y-yi)
در این فرمول n تعداد نقاط است ، y پاسخ اصلی و yi مقدار پیشبینی شده برای xi است. حالا اگر بتوانیم کمترین میزان ممکن یا همان مینیمم MSE را پیدا کنیم، در نتیجه میتوانیم خطی را رسم کنیم که کمترین خطا را دارد. یا به عبارتی بهترین پیشبینی و بهترین فرمول.
۳. بهینهسازی تابع هزینه با استفاده از گرادیان نزولی
حالا برای پیدا کردن کوچکترین میزان «میانگین مربعات خطا» یا همان MSE میتوانیم به سراغ روش «گرادیان نزولی» یا Gradient Descent برویم. این روش یکی از روشهای پرکاربرد برای بهینهسازی تابع هزینه است. در این روش ما از فرمول MSE نسبت به هرکدام از متغیرهای مستقل مشتق جزئی میگیریم.
گرادیان نزولی با محاسبه مشتقهای جزئی تابع هزینه نسبت به ضرایب (b0 و b1) شروع میشود تا جهت حرکت به سمت کمینه را پیدا کند. برای هر ضریب، مقدار زیر بهروزرسانی میشود:

در این فرمول α یا آلفا نرخ یادگیری است و سرعت حرکت به سمت کمترین میزان را کنترل میکند. نرخ یادگیری عددی کوچک است که تعیین میکند در هر گام چقدر به سمت پایین برویم. اگر این مقدار خیلی بزرگ باشد، ممکن است از نقطهی بهینه بگذریم و اگر خیلی کوچک باشد، مدل کندتر به نتیجه میرسد.
ایدهی اصلی این روش شبیه به پایین آمدن از یک تپه است: اگر بخواهیم به پایینترین نقطه برسیم، در هر قدم جهت شیب را دنبال میکنیم و آرامآرام به سمت پایین حرکت میکنیم.
در یادگیری ماشین، این روش با تنظیم و تغییر مقادیر پارامترهای مدل عمل میکند. مدل با استفاده از گرادیان کاهشی، در هر مرحله مقادیر پارامترها را کمی تغییر میدهد تا تابع هزینه یا خطا کمتر شود. با تکرار این فرآیند، مدل به نقطهای میرسد که خطا کمینه است و پیشبینیهای دقیقتری انجام میدهد.
۴. تفسیر مدل و استفاده از آن برای پیشبینی
پس از این که مینیمم MSE پیدا شد یا و بر اساس آن توانستیم ضرایب را پیدا کینم، حالا میتوانیم بگوییم که بهترین خط رگرسیون را بدست آوردهایم. این خط بر اساس این دادهها بهترین نتیجه و پیشبینی را به شما میدهد. حالا شما میتوانید از مدل استفاده کنید و دادههای بدون نتیجه را به این مدل بدهید و پاسخ را دریافت کنید.
۵. ارزیابی عملکرد مدل
ارزیابی مدل در یادگیری ماشین یعنی بررسی این که مدل چقدر خوب یا دقیق کار میکند. این کار با استفاده از دادههایی که مدل آنها را قبلاً ندیده انجام میشود تا ببینیم چقدر درست پیشبینی میکند. در این مرحله، با معیارهای خاصی مثل دقت، خطا یا صحت، عملکرد مدل را میسنجیم.
به بیان ساده، ارزیابی مدل مثل امتحان دادن است؛ مدل با دادههای جدید امتحان میدهد تا بفهمیم آیا واقعاً یاد گرفته یا هنوز نیاز به بهبود دارد. این کار کمک میکند تا نقاط قوت و ضعف مدل را بهتر درک کنیم و اگر لازم باشد، آن را بهینه کنیم. به عنوان نمونه یکی از معیارها برای اطمینان از دقت مدل «ضریب تعیین» است که میزان همبستگی بین پیشبینیها و مقادیر واقعی را نشان میدهد. مقدار R^2 بین ۰ و ۱ است و هرچه به ۱ نزدیکتر باشد، نشاندهنده دقت بالاتر مدل در توصیف دادهها است.
یک مثال کاربردی از رگرسیون خطی
یکی از کاربردهای بسیار مهم رگرسیون خطی، پیشبینی قیمت است. احتمالا تا به حال سامانهها و وبسایتهایی را دیدهاید که مشخصات ملک شما را از شما میپرسند و بر اساس آن قیمتی برای آن تعیین میکنند.
در این روشها آنها ابتدا پارامترهای مستقلی مانند محله، متراژ، تعداد اتاق خواب، سن بنا، تعداد پنجره و … را به عنوان متغیر مستقل در نظر میگیرند. این متغیرها هستند که قیمت نهایی خانه را مشخص میکنند. نکته مهم این است که هر متغیر به میزانی در قیمت نهایی خانه تاثیر گذار است. مثلا محله و متراژ تاثیر بیشتری دارند ولی تعداد پنجره تاثیر کمی دارد. از همین رو هر کدام از آن ها یک ضریب دارند. هرچه ضریب بزرگتر باشد، یعنی تاثیرگذاری آن متغیر بیشتر است.

اما چگونه این ضرایب را بدست آوریم؟ کافیست سری به املاکیها بزنیم و آمار خرید و فروش خانهها را برداریم بر اساس معاملات قبلی و این رگرسیون، میتوانیم طبق رویهای که در بالا توضیح دادیم، این ضرایب را پیدا کنیم و حالا وقتی میخواهیم قیمت خانهای را حدس بزنیم، کافیست محله و متراژ و … را در این مدل وارد کنیم تا یک پیشبینی از قیمت به ما بدهد.
رگرسیون خطی چه کاربردهایی دارد؟
- پیشبینی قیمتها: رگرسیون خطی به تحلیلگران کمک میکند تا قیمتهای آینده داراییها مانند سهام، مسکن یا کالاها را پیشبینی کنند. با استفاده از دادههای گذشته و متغیرهای مرتبط، میتوان الگوهای قیمتی را شناسایی و به برآورد قیمتهای آینده پرداخت.
- تحلیل اقتصادی: این روش در تحلیل روابط بین متغیرهای اقتصادی مانند درآمد و هزینهها، یا تولید ناخالص داخلی و نرخ بیکاری مورد استفاده قرار میگیرد. با مدلسازی این روابط، اقتصاددانان میتوانند تأثیر تغییرات یک متغیر بر دیگری را تحلیل کنند و به پیشبینیهای اقتصادی بپردازند.
- پیشبینی فروش: شرکتها میتوانند از رگرسیون خطی برای پیشبینی میزان فروش محصولات خود بر اساس عوامل مختلف مانند قیمت، تبلیغات و فصل استفاده کنند. این تحلیلها به مدیران کمک میکند تا استراتژیهای بازاریابی مؤثرتری را توسعه دهند.
- تحلیل سلامت: در حوزه پزشکی، رگرسیون خطی برای بررسی رابطه بین متغیرهای سلامتی مانند فشار خون، سن و دیگر عوامل خطر استفاده میشود. این مدلها میتوانند به شناسایی عوامل مؤثر بر بیماریها کمک کرده و در نهایت به بهبود روشهای درمانی منجر شوند.
- مدلسازی آب و هوا: رگرسیون خطی به دانشمندان هواشناسی کمک میکند تا الگوهای آب و هوایی را بر اساس دادههای تاریخی پیشبینی کنند. این روش میتواند به پیشبینی دما، بارش و سایر شرایط جوی کمک کند و در برنامهریزیهای مرتبط با کشاورزی و منابع آب موثر باشد.
- تحلیل ورزشی: در دنیای ورزش، رگرسیون خطی برای پیشبینی عملکرد ورزشکاران بر اساس متغیرهای مانند سن، تجربه و تمرینات به کار میرود. این تحلیلها به مربیان کمک میکند تا استراتژیهای بهینهای برای بهبود عملکرد ورزشکاران توسعه دهند و در نهایت به موفقیت تیم کمک کنند.
خلاصه
رگرسیون خطی، یکی از سادهترین روشهایی است که در دنیای هوش مصنوعی بکار گرفته میشود. با وجود سادگی بسیار، این روش همچنان کاربردهای بسیاری دارد. در بسیاری از فضاها که شما حجم قابلتوجهی از دادههای برچسب دار دارید و احساس میکنید میان ویژگی و برچسب ممکن است یک رابطه خطی باشد، به راحتی میتوانید از این روش استفاده کنید.
هرچند که روشهای بسیار دقیقتر و پیچیدهتری امروزه وجود دارد، اما این روشها همچنان در بسیاری از زمینهها کاربرد دارد.



































